
Trippr audio programming: Interpolated noise (part 4)
December 11, 2018 - Jos van Tol
As a little addendum I'll talk a bit about the secret noise I've added to the Trippr tone. It's silently there in the background. It's a version of Brownian noise by interpolating between random points in the signal.
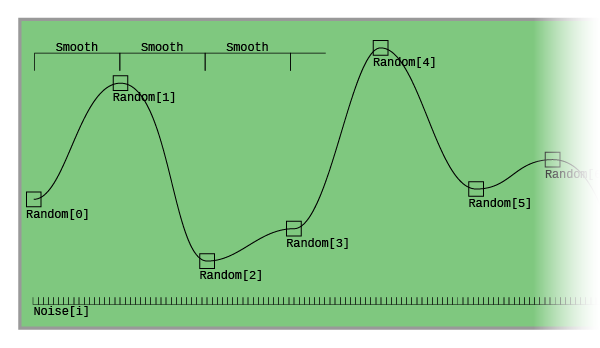
We'll divide our buffer in evenly spaced blocks. We'll use a power of two so it'll fit nicely. In this case 64 (26), which will fit sixteen times in our buffer of 1024 (210) samples. These blocks will smoothly step between random points. We'll save all our samples in an array called Noise.
uint32_t Smooth = 64;
float Random[SamplesToWrite / Smooth];
int16_t Noise[SamplesToWrite];
Now we'll get random values between -1 and 1 to interpolate between. We will have to set the first and last one to 0 so the ends will always meet nicely.
Random[0] = 0.0f;
Random[SamplesToWrite/Smooth] = 0.0f;
for (uint32_t i = 1; i < SamplesToWrite/Smooth; i++)
{
Random[i] = (float)rand()/(float)RAND_MAX * 2.0f - 1.0f;
}
Now we'll use the Smoothstep() function to interpolate between these points. Then multiply these by the 16-bit min/max 32,767.
for (uint32_t i = 0; i < SamplesToWrite/Smooth; i++)
{
for (uint32_t j = 0; j < Smooth; j++)
{
Noise[i*Smooth + j] = (32767 * Smoothstep(Random[i], Random[i+1], Smooth, j);
}
}
The Smoothstep() function I got from this great site. This is it:
float Smoothstep(float A, float B, uint32_t N, uint32_t i)
{
float t = i/(float)N;
t = t * t * (3 - 2*t);
return (1.0f -t)*A + t*B;
}